Quadratic Magic!

I'm working at MOE now, and I'm drowned out by the boredom here! But after some reflection, I find the method of differences a rather interesting tool to help me derive some basic ‘A’-Levels identities and general formulae, such as a general expression for the sum as shown below:


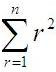
Well, I guess I’d call this the quadratic series, and it occurs rather frequently in applications, and thus it’d pay to know how to derive a general formula for this sum. We start off by writing down the general term expression to work with first:


Of course, you might wonder why I wrote down the general term as a cubic term, but be patient! Next we find the difference as such:


Ah hah! Notice that by using a cubic term, we effectively forced out the quadratic term (together with a linear and constant term)! Looks really easy and neat so far! Now, the next step, as always, is to sum up the above difference to n terms:


Now, we’ve gotten ourselves a nice equation; to make use of this equation, we notice that we can simplify the two summation terms at the top of the above expression as such:


Voila! It becomes a sum of a quadratic equation! So if we rewrite this properly, separating individual terms into their sums, we have:


On the left hand side, we notice that the last two terms are particularly easy to reduce into simpler expressions, as such (well, you should know this if you’ve been through ‘A’-Levels!):


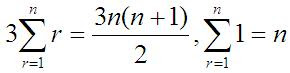
So if we now make a simple substitution, we obtain:


And yes, a simple, neat and beautiful proof for the quadratic series! :) Heh.