How Mean Are They?

Recall that in an earlier post, I pointed out that there were four different kinds of means that commonly pop up in physical situations, and to recap your memory, they are:

The Arithmetic Mean

The Geometric Mean

The Harmonic Mean

The Power Mean

Oh and before anything, I shall just assume both numbers are positive, so it simplifies my working. :)

And of course, I’ll now endeavour to show the relative magnitudes of the above means I’ve stated, and I’ll start with the power mean (I’ll consider a specific one, the quadratic mean) and geometric mean first, since these two are easiest to compare:



Another easy pair is the arithmetic mean and the geometric mean:


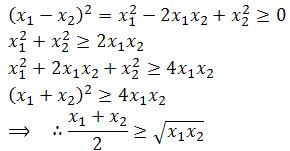
The next easy pair should then be the arithmetic mean and the quadratic power mean:

Notice that I’ve used the same inequality over and over again, namely:

Is that amazing, or what? Let’s now recap:


So this leaves us with the harmonic mean, which can be a rather nasty affair, but with some tricks again, we’ll see:

There you have it: by proving that the geometric mean is greater than the harmonic mean, we no longer have to prove the other pairs of means, because the geometric mean was the least in our previous analysis. And therefore, we can now say:


So why have I determined the order of the magnitudes of the different means? Well, it's to show you that there is no such thing as "one mean is more mean than the other"; their magnitudes can still differ considerably from one another! Therefore, we can't really say one mean is better than the other, but rather, we have to look at the situation, and what the situation calls for, before we choose the appropriate mean to use.

Another conclusion can be drawn if you look at their mathematical structure: if you look at the geometric mean, one may think it's not giving equal weightage to both numbers; but what if you think about the powers? Multiplying two numbers together means you're adding their powers together, and taking the square root halves their powers added, and thus the geometric mean effectively gives you the mean of the powers of the two numbers.

How about the harmonic mean? It's interesting, because the product of the two numbers is weighed by the sum of the two numbers - it is as if this mean weighs the two numbers according to how big they are, or how small they are! I'll speak more on this in a later post.

And all of these things are nice to chew upon. Heh. :)