Harmony

I’m going to analyse a little bit of the nature of the harmonic mean, but first, let us consider where in nature does this type of averaging take place. In order to do so, let us consider a very simple PSLE question:

“I want to go to the beach from my house, and I travel there at an average speed of 30 km/hr. Going home, I travel back to my house at an average speed of 20 km/hr. What then is my overall average speed?”

Interesting enough, 95% of everyone I’ve asked (to be fair, I asked them to give me an intuitive answer without working) gives the answer 25 km/hr, the average of 30 and 20. But remember, this is the arithmetic mean – is it truly the answer? Well let’s do some algebra to find out:


Doesn’t the last statement look familiar? Let’s contrast what we have with the harmonic mean:


Yes! You have just used the harmonic mean to calculate the overall average speed! And the normal arithmetic mean will not work in this case.

Well apart from the fact that algebra obviously must work, is there a physical reason as to why we used the harmonic mean? There is! Recall I mentioned that the harmonic mean is a special mean that weighs the magnitude of the two numbers we’re averaging? Haha, yes, but how exactly does it weigh? I’ll give you an example; let’s say I have the following harmonic mean:


And I say



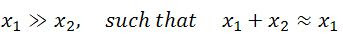
And of course, what does this mean? It means that we can then neglect the presence of the second x value in the denominator:



Therefore we see the harmonic mean actually weighs out both numbers and gives a number that sort of “favours” (technically favour isn’t the word but never mind) the smaller of the two numbers!

With this concept in mind, we go on to note that harmonic means typically occur in time-based problems. The above PSLE question was one good example. Another example is the concept of reduced mass in a diatomic molecule, where we say the reduced mass is given by the harmonic mean:

So what happens if say, the second mass (i.e. one of the atoms in the diatomic molecule) is super huge and massive? Then we can neglect the first mass in the denominator and say that:


So what does this physically mean? It means that most of the time, mass 1 is doing the vibrating of the molecule – this makes sense, because lighter atoms move faster, and thus mass 1 should be doing most of the vibrating of the diatomic molecule.

In relation to the PSLE question, the harmonic mean favours the smaller number, and thus gives us a value of 24 km/hr, which is closer to 20 km/hr. Notice that the person travelled to the beach at 30 km/hr and then back at 20 km/hr – so I ask you, which speed is used for a longer time? That’s right, the 20 km/hr speed is being used for a longer time! And this is the crux! The harmonic mean actually deals with the number that has the greatest time concentration (time concentration isn't exactly the right term here, but oh well)!

For instance, in a diatomic molecule, the smaller mass is moving most of the time, and thus the harmonic mean favours it. In the PSLE question, you spent more time moving at 20 km/hr, so the harmonic mean favours it. In another physical situation where you have rotating masses, the reduced mass favours the smaller one, because the smaller mass is moving most of the time, and the larger one is effectively stationary.

Therefore, the harmonic mean actually weighs the two quantities in accordance with how much time has been associated with each of the quantities. Oh well, this has been a weak, incomplete and unmathematical justification of the true nature of the harmonic mean, but it’ll do – I’m super tired from work, heh.