2nd Round

This is the second question of the 1st IPhO - try it for kicks! (Click on it to view the enlarged picture - same for all other pictures in this post!)

--------------------------------------

I actually remember doing this in Physics ‘S’ paper! Haha. So let’s give it a try, using my well, noob method. Let’s consider a simple system at the start first:

Obviously the resistance here is just the simple sum of two resistors in series:

Let’s continue to add two more resistors; notice that I’ve renamed one of the resistors x (you’ll know why in a second!):

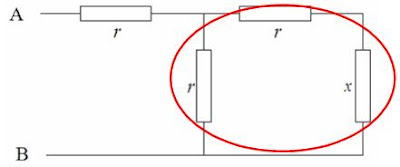
This is a little trickier; the resistance here must take into account the parallel circuitry, which I’ve circled out in red. If you can’t see this, well, let me redraw it in a more accessible manner:

And of course, if you still remember the formula for parallel resistors, this new set-up has a fairly easy to calculate expression for its resistance:


And then let’s do one more addition of a branch to see how everything adds up, to understand how I’m going to simplify the situation:

Well, without redrawing it, I’d expect you to say that the set-up now consists of two parallel set-ups. For those who can’t see yet, I’ve tried to point out using circles again. Look above at the blue circle; I can represent this as a resistor x, and then the diagram is simplified into:

And what do you notice? Haha, we’ve already obtained the resistance for this, which was determined earlier to be:

So what’s x? Well, let’s find out; referring to the blue circle, I see that x’s resistance is simply equivalent to a set of parallel resistors:

Okay, so that you’ve roughly got my trick of simplifying, let’s do a long set so that you’ll be seeing what I’m seeing:

Let’s do the red circle first, and let’s call this new resistor a:

Now, treating the red circle as a resistor a, we can simplify the diagram into:

Alright, so now let’s do the blue circle and let’s call this new resistor b:


So now we can simplify again:


And now let’s do the green circle and let’s call this resistor c:


And now, let’s simplify again:

This couldn’t be simpler, and let’s do the orange circle this time and call it a resistor d, and find its resistance:

With this, we can then simplify our diagram as:

And the overall resistance is therefore simply:

Now, if you haven’t seen or noticed the pattern yet, let me just write out everything in full:


What a monster! You may want to view it in full size, haha. Notice that there is a repeating unit! And if the series goes on and on indefinitely, let me just re-write it in a more digestible way:


Can you spot the repeating unit yet? Haha. If you haven’t spotted the recurring unit yet, it’s simply this monster right here:

But what is this creature? Notice that the overall resistance R is just the repeating unit:

So how do we solve this thing? Well, algebra gives us a good method:

And then now we manipulate this expression into a quadratic equation, as such, to obtain R:

Which can then be solved using the standard quadratic equation (notice I’ve rejected the negative answer since no resistance is negative):

And as some of you might have already noticed, the Golden Ratio (phi) appears in the answer:

Such that:

Well, what is the Golden Ratio? Let’s leave that for another entry, because I’m absolutely tired of typing out equations and expressions for the day. I’ll give a hint though; recall the Fibonacci sequence as:

If you look closely, each succeeding term is obtained via addition of its two preceding terms. Well, if you take any term and divide it by its preceding term, you’ll obtain a number close to the Golden Ratio (phi). Let’s say we take 89 and 55:


And this ratio gets increasingly closer to the Golden Ratio as one continues on into the series.

And wow! What a lengthy post! And it's rather strange isn't it? Then adding more and more resistors forces your resistance into a fixed, finite value instead of an infinite resistance, and the fact that the Golden Ratio pops up in such an instance! Simply amazing! :p