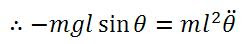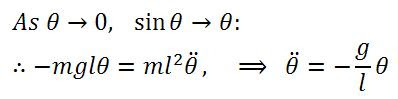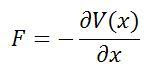Ass'N Tool (Pun Intended!)

Well, so we all know (or do we? Haha!) that the famous SN2 reaction proceeds via a 'backside' attack.

Yep, you got that right - when the nucleophile attacks an alkyl halide, it hits it right on its gluteus maximus (actually, I see it from another angle, but never mind).

And of course the age-old question: why? Why in particular, the 'backside'? Well, everything will be made clear with Molecular Orbital theory, so let us consider what the LUMO (Lowest Unoccupied Molecular Orbital) of a typical alkyl halide (in this case, chloromethane) looks like:


Notice the huge lobe on the 'backside' of the carbon atom? That's where the nucleophile attacks if if wants to bond to the carbon atom - by donating electrons into this antibonding orbital, the carbon-chlorine sigma bond effectively breaks, and a SN2 reaction ensues.

Ah well. I probably haven't explained in detail enough. But hey, I'm tired. :)

Recollection

I know I've asked this before, but it keeps coming back to me, again and again:

Does a proton possess orbitals?

If you say I'm silly, then consider the thousands of Chemists worldwide who speak of the hydrogen ion (H+) as having orbitals.

Isn't a hydrogen ion a proton?

But isn't a proton a free particle by itself?

Quantum mechanics is just plain weird, period. :)

Conquering the FORTress

Mr Yeo has successfully written his quadratic equation solver program, so now all you people out there can use it for their homework. :)

And that's the first step to conquering Fortran! :)

Unfortunately, Yahoo Geocities is closing its server this October, so I shan't bother to post it up; will probably do so when I've found another host. :)

So many smilies. Yay! :)

Water Me Down!

You know, I’ve always wanted to construct a Walsh Diagram for a simple molecule? So what exactly is a Walsh diagram? Well, let me illustrate using water as an example; one should know that water has an equilibrium geometry that is bent, with a H-O-H angle of 104.5 degrees as such:

And of course, the other limiting (non-equilibrium) geometry would be a linear geometry with a H-O-H angle of 180 degrees as follows:

So now the question is, why is the former geometry adopted by water molecule? Phrasing this question another way: is it such that the energy of the water molecule is lower when it has a H-O-H bond angle of 104.5 degrees?

Well, the easiest way to find out whether this is true or not (not so much why it is true!) is to plot a graph of the energy of the water molecule against the H-O-H bond angle.

Now usually you wouldn’t be able to calculate the total electronic energy of the water molecule by hand, but since I’m bundled up with this molecular calculation suite called Gaussian03 (yes, I know the latest version is G09!), I’ve performed the calculations using my trusty laptop.

So here’s the graph, or like how they call it, the Walsh Diagram for the water molecule (click to enlarge):


This graph actually shows that the 104.5 degrees H-O-H bond angle gives rise to a lower total electronic energy of water than the linear geometry! So be convinced! That the Singaporean education system isn't wrong! :)

So the next step comes in explaining why that's the case.

Another time. :p

And all calculations were clumsily performed with a minimal STO-3G basis set using the Hartree Fock level of theory, which merely took 5 seconds or so for each single point energy calculation.

Yay! Time to sleep. :)

Don't Point So Much!

I'm undertaking this module on group theory, and I noticed something that I never really thought about because I just took things for granted. Now, given that:


And given that the first two results are definitely correct, what can one say about the third?


And well well, here are two molecules where students usually assign the wrong point group to:




If you'd like to try, then don't play cheat and figure it out from scratch! :)

----------------------------------------------

Because I am the lazy person that I am (I'm too tired, :p), the answers are as follows without explanation or elaboration:

Satisfaction

I've been feeling rather dry lately, but I'd just like to say:

Science is nothing more than intellectual satisfaction to me. It represents not the truth, neither is it any philosophy; it is simply a set of tools, principles and logic obtained from empirical evidence that appeals to the human mind in such a way that I am excited by it.

That being said, truth is not discovered, but revealed only to those who seek it. :)

So continue to seek Him YYK. :)

Druggie Druggie Addict!

There's a hidden birthday message, can you find it?

So here's the case; as is the case with the USA, Singaporean soldiers are not allowed to take illegal drugs (besides the usual smoke I guess, which is perfectly legal). The question that I pose to you now, is:

If you'd like to do a survey to find out how many Singaporean soldiers consume illegal drugs, how would you do it?

You must keep in mind that if they do confess or are caught answering "Yes", then they will face the death penalty or some other kind of huge fine. The nice guy you are, you'd want to come up with a way to prevent this, and yet come up with some sort of estimate of figures.

Knowing this blog, it's definitely a statistical trick that you'll have to employ, but what? Heh.

-------------------------------------------

Well, the thing is, you've got to let them confess in secret, but yet you have to know what they confessed somehow. But you need to ensure their anonymity and safety as well!

As such, leaving any high-technology mind reading devices out, we are left with no choice but to play Jedi mind tricks.

Yeah right. We just use what we learnt in high school - that's right, simple statistics, for a good estimation.

We come up with three types of cards, as shown (of course their backs will be all of the same colour):


Each type of card is associated with one type of question - these questions need not be written on the card, but may be posed to the soldiers verbally. Now, to ensure that the soldiers draw out a card at random, so the chance of drawing a red, blue or green card is 1/3 for all, we have say, a good number of cards (say 72 cards) laid down like this:


So now, the chance or probability that any soldier draws the green, blue or red card, is exactly 1/3, even if he or she has a propensity or tendency to draw from the corners or from the middle of the deck. Make sure that the cards are laid in the order as shown for the probability to be true.

Let's give it a go; let's say for example, that out of 12000 soldiers who were surveyed, 5600 of them answered "Yes". Assuming all soldiers are sane, and that they completely understand English and are well, disciplined enough to not want to play with the system, they'll be truthful.

Therefore, all "Yes" replies must mean that the soldiers either chose the red or blue card.

Since 12000 is a huge enough number, and this is a fair test, we should be confident enough to say that on average, we expect 4000 soldiers to say "Yes" to the question of whether "Is this card red?"

If that is the case, then we expect that on average, at least 1600 soldiers do take some kind of illegal drug.

On the other hand, we also expect 4000 soldiers to say "Yes" to the question of "Do you take drugs?"

So what does all these mean? It means that on average, we expect at best, 1600 soldiers to be taking drugs, but at worst, 4000 soldiers to be taking drugs.

It'd be good to perform another test on another group first, to obtain the standard deviation! Haha.

So... what do you think? Aren't statisticians rather useful? Heh.

Representations

Well, for those who have no knowledge of matrices, here's a challenge I have for you; given that the rules of 2x2 matrix mutliplication are summarised as such:


Can you find me a 2x2 matrix, such that when it's multiplied by itself, yields:


There's about 10000000000000000000000000000000000 such matrices by the way. So if you can find 1, and you think you're smart, think again. Haha.

------------------------------------------

Well, even though this post has been here for the longest time, it seems that no one has ventured beyond perfunctory reading, so I guess I'll just carry on.

One possible matrix would be:


And another would be:


There's actually a pattern: the number in the upper left and lower right positions are the same! But of course, you'd need the right combination. Heh. Can you find any more? There's probably a million more of these, haha.

Stay Still!

I think I’ll go into the idea of stationary states today; what exactly is a stationary state? Well, it’s essentially a state of a system, where the energy of the state remains constant over time. Defined more rigorously, it’s a state where the expectation values of observables remain constant over time.

For instance, let us take a look at the particle-in-a-box wavefunctions (as functions of time and position):


So let’s consider the probability density function of finding the particle within the box:


Notice that the phase factors (exponential time factors) cancel out when the complex conjugation is taken and multiplied! That is, the probability density function isn’t a function of time! It’s solely a function of position and thus, doesn’t vary with time.

How about the expectation value of the position? Well let’s take a look:


Hey! It turns out that the expectation value of the position doesn’t depend on time as well! So, it turns out that for all states of the system that are eigenstates (that is, if the system exists only as an eigenstate), the state is a stationary state!

So what isn’t a stationary state? Well, let’s look at linear combinations of eigenstates; we know that any linear combination (properly normalized of course) of eigenstates will still result in an arbitrary state that is a solution of the Schrödinger equation, so let’s try a positive linear superposition of the ground state and first excited state (I’ve normalized it for all of you already):


Let us now evaluate the probability density function (click on it to enlarge it):


Notice that now the probability density function is a function of time as well! The time phase factors no longer cancel out! It turns out that for any linear combination of eigenstates, the state will no longer be a stationary state – and therefore observables like its energy, momentum and even position will not have time-constant expectation values.

If you’ve heard physics professors go, “It’s all because of the cross terms!” this is what it means. Haha.

Postulato Negativito!

So I was looking, and I was just a little bit amused:

"So... there are two types of fundamental postulates in science. The first type is the self-evident kind, like how heat flows from hot to cold regions. The second type is one that is more subtle, and needs to be unfolded in a series of arguments before you get the point of it all."

And why am I laughing?

"Unfortunately, in Quantum Mechanics, the fundamental postulates all belong to the second type."

Lol!

Time Evolution

So if you look at it this way, then the time evolution of the wave function of a system is no more than an evolution that is governed by the energy of the system:


Then only separating out the time-dependent wavefunction:


It would appear that the time evolution of a system lies only in the changing of the phase of the system!

Strange. Weird. I still don't get what this means, haha.

Double Pendulum Revisited

Remember this post: http://wulidancing.blogspot.com/2008/07/double-pendulum.html?

Well, it turns out that you don't really need any high-level mathematics for this question, and I'm just wondering how come I didn't figure it out at that time, haha. So here's the whole set up again:


It'd be useful to see that the equilibrium position should have zero gravitational potential energy:


The trick to solving this question is to lift each pendulum up one after the other; so let's give the first pendulum a push and see what happens to the potential energy:


Notice that both pendulum bobs are raised by the same length, which explains the coefficient of '2'. Now let's give the lower pendulum another push and let's see what happens:


Notice that we've just added another term to the potential energy, and this time the coefficient is '1' because only one bob is raised.

Quite easy right? Haha.

Lagrangian in Action

As a follow up to my previous post, let's see some Lagrangian Mechanics in action, with the use of a very easy example - the simple pendulum! So let us consider the following set-up:


For your convenience, I've worked out the various quantities to take note already, and I've labelled all of them on the above diagram. Now, with all of these observables in place, we can now write down the Lagrangian immediately:


Notice that I'm no longer using the x coordinate! This explains why the Lagrangian is so versatile, because it can be expressed in terms of any general coordinate, and still work! So given this, let us work out the Euler-Lagrange Equation:


And we see that if we equate the two derivatives, we obtain the equation of motion:


Notice that we didn't even have to go about resolving out the various forces, like tension or weight or whatever! It's really easy with Lagrangian Mechanics!

I believe your teacher might have told you to "only make small oscillations when setting up the pendulum", and the rationale for that being that "small oscillations result in simple harmonic motion." But how?

Easy, let us consider small angular displacements, and our equation of motion automatically reduces to:


Voila! Notice that the second derivative with respect to time of the angular displacement (i.e. angular acceleration) is now directly proportional to the angular displacement! This is the very definition of simple harmonic motion!

Haha. Easy right? Lagrangian Mechanics really simplifies a lot of things. :)

1, 2, 3... Action!

Last night I was getting down to understanding the Lagrangian as it is used in Classical Mechanics, which is something I’ve been putting off for quite a while now; but taking a closer look at it, it doesn’t seem as tough as I thought it’d be! Well well, so how does one start?

Well, a proper derivation proved too tedious for me to want to type it out (I tried deriving it for my friend Shaun, but I gave up halfway because it’s really too long and I was lazy, haha!) so here’s a really general derivation, which needs some prior knowledge of calculus of variations.

But I think all of you are smart. So I’m going to go ahead with this general derivation. Haha.

Alright, let’s start with the following equation, known as the Euler-Lagrange Equation:


As above, we have an equation that is pretty much obvious: it’s simply a differential equation that involves a function of three variables x, y and y’ (the derivative of y with respect to x).

Now, for any function F(x, y, y’) that fulfills this condition, we can immediately say that over the interval as shown below:


I won’t be explaining why this is the case, because it took me quite some pages to type out and I don’t think I’m in the mood to type everything out for this blog post, haha. So please do accept this for the time being!

So what does this have to do with the Lagrangian function in Classical Mechanics? Oh yeah, what is the Lagrangian?

Well, it’s simply this function right here:


Where T is the total kinetic energy and V is the total potential energy of the system. Notice also that:


So we now rewrite the Lagrangian as:


Now, let us consider the following derivatives of the Lagrangian:

Now for all conservative central potentials, which we are all familiar with, we know that:


That is, the negative of the gradient of the potential energy is the force acting on the system at that position (JC students might remember this from basic Gravitational Theory). So let’s keep this in mind first! Now onto another derivative of the Lagrangian:


Of course, we know that:


Which is acceleration! Let us now put everything together:


Now let us compare the Lagrangian differential equation with the Euler-Lagrange equation:


Hey! Doesn’t this mean that the Lagrangian should then imply that the following integral is a minimum:


This integral is known as the action; notice that Newton’s Second Law is actually an Euler-Lagrange Equation when it is written in the form of the Lagrangian, which in turn means that the above integral, the action, is to be a minimum.

This came to be known as what is now called the Principle of Least Action.

And that’s about as watered-down as I can make it for all of you, haha.

Separate Them!

I would like to highlight in this post, a nice mathematical technique known as separation of variables, which reduces a more complicated partial differential equation into a less complex ordinary differential equation. To illustrate this technique, I shall be using the time-dependent Schrodinger wave equation in 1 dimension, which is as follows:


This equation tells us that the time evolution of the wavefunction depends on how the Hamiltonian operator acts on the wavefunction. That is, the time evolution depends in some manner, on the energy of the system.

With that, we shall now consider the Hamiltonian operator acting on the wavefunction:


However, in most cases, the potential is independent of time, say like how an electron always orbits around a fixed centre of charge; therefore, we indicate this by re-writing:


Notice now that the potential function only depends on the position coordinate, and not time. Now, we can write out the full time-dependent wave equation as:


In quantum mechanics, it turns out that the overall time and position dependent wavefunction can be factored out into a product of separate time wavefunctions and position wavefunctions. That is, we can now write:


This assumption (generally valid when the potential is not a function of time) leads to the technique known as separation of variables, where you effectively factor out one variable from a function. And if we make the substitution, we see that:


Dividing throughout by φ(x)τ(t):


Alright! Now on the left we have a function depending solely on time, and on the right a function depending solely on position! Notice that we have separated the variables! So what’s so good about this you say? Consider this:

‘If I vary x only, then only the right hand side of this equation should change, since the left hand side doesn’t depend on time. However, if the left hand side doesn’t change and remains constant, so should the right hand side! This means that both sides are actually equal to a constant!’

With this revelation, can you fashion a guess as to what this constant might be?

If you said energy, you are absolutely right! We can now equate both sides to the energy of the system:


Also notice that the equations are no longer partial differential equations, but ordinary differential equations! We’ve made life simpler! Hurrah!

Let us look at the time-dependent wavefunction:


Voila! The time-evolution depends on the energy of the system as shown! Now, you might be wondering about the position-dependent wavefunction, so let me rearrange it as shown:


Hark! Isn’t this the usual time-independent Schrodinger wave equation that we always see? Haha.