Lagrangian in Action

As a follow up to my previous post, let's see some Lagrangian Mechanics in action, with the use of a very easy example - the simple pendulum! So let us consider the following set-up:


For your convenience, I've worked out the various quantities to take note already, and I've labelled all of them on the above diagram. Now, with all of these observables in place, we can now write down the Lagrangian immediately:


Notice that I'm no longer using the x coordinate! This explains why the Lagrangian is so versatile, because it can be expressed in terms of any general coordinate, and still work! So given this, let us work out the Euler-Lagrange Equation:


And we see that if we equate the two derivatives, we obtain the equation of motion:


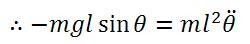
Notice that we didn't even have to go about resolving out the various forces, like tension or weight or whatever! It's really easy with Lagrangian Mechanics!

I believe your teacher might have told you to "only make small oscillations when setting up the pendulum", and the rationale for that being that "small oscillations result in simple harmonic motion." But how?

Easy, let us consider small angular displacements, and our equation of motion automatically reduces to:


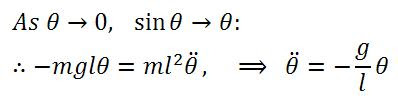
Voila! Notice that the second derivative with respect to time of the angular displacement (i.e. angular acceleration) is now directly proportional to the angular displacement! This is the very definition of simple harmonic motion!

Haha. Easy right? Lagrangian Mechanics really simplifies a lot of things. :)