1, 2, 3... Action!

Last night I was getting down to understanding the Lagrangian as it is used in Classical Mechanics, which is something I’ve been putting off for quite a while now; but taking a closer look at it, it doesn’t seem as tough as I thought it’d be! Well well, so how does one start?

Well, a proper derivation proved too tedious for me to want to type it out (I tried deriving it for my friend Shaun, but I gave up halfway because it’s really too long and I was lazy, haha!) so here’s a really general derivation, which needs some prior knowledge of calculus of variations.

But I think all of you are smart. So I’m going to go ahead with this general derivation. Haha.

Alright, let’s start with the following equation, known as the Euler-Lagrange Equation:


As above, we have an equation that is pretty much obvious: it’s simply a differential equation that involves a function of three variables x, y and y’ (the derivative of y with respect to x).

Now, for any function F(x, y, y’) that fulfills this condition, we can immediately say that over the interval as shown below:


I won’t be explaining why this is the case, because it took me quite some pages to type out and I don’t think I’m in the mood to type everything out for this blog post, haha. So please do accept this for the time being!

So what does this have to do with the Lagrangian function in Classical Mechanics? Oh yeah, what is the Lagrangian?

Well, it’s simply this function right here:


Where T is the total kinetic energy and V is the total potential energy of the system. Notice also that:


So we now rewrite the Lagrangian as:


Now, let us consider the following derivatives of the Lagrangian:

Now for all conservative central potentials, which we are all familiar with, we know that: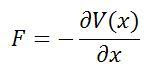


That is, the negative of the gradient of the potential energy is the force acting on the system at that position (JC students might remember this from basic Gravitational Theory). So let’s keep this in mind first! Now onto another derivative of the Lagrangian:


Of course, we know that:


Which is acceleration! Let us now put everything together:


Now let us compare the Lagrangian differential equation with the Euler-Lagrange equation:


Hey! Doesn’t this mean that the Lagrangian should then imply that the following integral is a minimum:


This integral is known as the action; notice that Newton’s Second Law is actually an Euler-Lagrange Equation when it is written in the form of the Lagrangian, which in turn means that the above integral, the action, is to be a minimum.

This came to be known as what is now called the Principle of Least Action.

And that’s about as watered-down as I can make it for all of you, haha.