The more accurate way to quote Newton’s Second Law, which holds for all situations, is this: the net external force on an object is the time rate of change of momentum of the object itself. And we express this mathematically as:

And I’ll illustrate the generality of this expression by using this to derive a relativistic expression for the acceleration of a body. Now, to start off, let us recall the relativistic momentum expression:

And therefore the rate of change of momentum of a body must be given by a direct differentiation with respect to time:

And if you simplify this, it becomes:

And we recognize two things, that is:
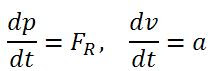
And therefore:

Notice that Newton’s Second Law no longer just involves the product of the mass and acceleration – this means that the expression F = ma is not a generally valid expression! And hence my conviction that Newton’s Second Law should be reformulated in terms of rate of momentum change instead.
Now, let us rearrange what we have above:

So let’s say you want to accelerate a body to the speed of light (c ms^-1), notice that as the speed v tends towards c, the acceleration tends to zero for a finite force:

So how do you accelerate something to a speed of c given that the acceleration fades away to zero when you near the speed of light? Easy, you use an infinite force! But is there such a thing as an infinite force? No! However, is there another way to go about it? Well, yes! Notice that as the mass goes towards zero:

Therefore, if the mass of a body is zero, then it is possible to accelerate the body all the way to the speed of light!
Ask yourself, what is the mass of a photon? :p It’s simply zero, which is expected! Otherwise it can’t go at the speed of light! :)