
How would you solve it? I mean, there’s always the conventional method of assuming a solution that has an exponential form, but did you know that you can treat this like a quadratic equation?
The method is known as the solution of second order differential equations via factorization, which isn’t really an original method thought out by me, but well, it helps to explain why the solution is of an exponential form. First of all, we factorize out the y term:
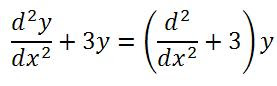
Then of course, we make a simplification; that is we allow:

And therefore we must insist that:

Of course, let us factorize this further:

In which case we must therefore have:

And of course if we solve for these two equations, we have:

And of course, the general solution being the sum of the two particular solutions we obtained earlier, from the principle of superposition for linear equations:

And if you only want a real solution, then:

And this explains why we always assume the solution is of an exponential form; simply because if you do solve it from first principles, it always is! :)

No comments:
Post a Comment