Newton's Legacy

Here’s something for you to think about – Newton’s Second Law is often quoted as the net external force on an object is the product of the object’s mass and its acceleration. Well I wouldn’t say that’s wrong, but that’s only truly correct in a classical sense. That is, the following equation only holds for non-relativistic speeds:


The more accurate way to quote Newton’s Second Law, which holds for all situations, is this: the net external force on an object is the time rate of change of momentum of the object itself. And we express this mathematically as:


And I’ll illustrate the generality of this expression by using this to derive a relativistic expression for the acceleration of a body. Now, to start off, let us recall the relativistic momentum expression:


And therefore the rate of change of momentum of a body must be given by a direct differentiation with respect to time:


And if you simplify this, it becomes:


And we recognize two things, that is:


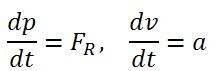
And therefore:


Notice that Newton’s Second Law no longer just involves the product of the mass and acceleration – this means that the expression F = ma is not a generally valid expression! And hence my conviction that Newton’s Second Law should be reformulated in terms of rate of momentum change instead.

Now, let us rearrange what we have above:


So let’s say you want to accelerate a body to the speed of light (c ms^-1), notice that as the speed v tends towards c, the acceleration tends to zero for a finite force:


So how do you accelerate something to a speed of c given that the acceleration fades away to zero when you near the speed of light? Easy, you use an infinite force! But is there such a thing as an infinite force? No! However, is there another way to go about it? Well, yes! Notice that as the mass goes towards zero:


Therefore, if the mass of a body is zero, then it is possible to accelerate the body all the way to the speed of light!

Ask yourself, what is the mass of a photon? :p It’s simply zero, which is expected! Otherwise it can’t go at the speed of light! :)

God's Thoughts

"I want to know how God created this world. I am not interested in this or that phenomenon. I want to know His thoughts, the rest are details." - Albert Einstein, Jewish Physicist

And this is what one of the greatest minds who ever lived on this Earth once said - and I find it so encouraging that even a giant like Albert Einstein was after God's heart and mind, and how his Creation came into place.

I'd like to emphasise that all Science around us, all Mathematics, is only but an attempt to describe and understand this world, which is based on the laws that God engineered for all of us. Seeing how this intricate clockwork has come together, His handiwork is truly in the firmaments. :)

*Note: Albert Einstein wasn't a Christian even though he pursued the thoughts of God.

At The Speed of Light

It's now 8:00 am in the morning, and I just had this flash of inspiration whilst in the toilet; not too glamourous a situation for a brainwave, but oh well. Hopefully you all can understand what I'm about to type out.

Many years ago, Einstein as a young lad was thinking to himself: "What would happen or what would I see if I travelled at the speed of light? Would I see light waves or photons freeze in their tracks because I'm moving just as fast as them and thus the relative velocity between them and me is zero?"

And many years later, Einstein was convinced that no matter how fast one travels at, even at the speed of light, one will still see light travel at the speed of light.

Why?

Well, to first understand the situation, you must first understand the fundamental problem in Einstein's gedanken, that is, can you even see a stationary light wave?

The answer is a resounding and definite NO! Light, being composed of photons, are massless particles. From Einstein's mass energy equation, we therefore know that the total energy of a photon must be composed of its momentum-energy, that is, its kinetic energy, because it has no mass at all.

Now, to view a photon that is stationary, is then to view a photon without its kinetic energy - by denying a photon its kinetic energy, one essentialy annihillates that photon from sight. By travelling up to the speed of light, and to insist that one can still see light, then the light waves that one sees while travelling at the speed of light, must still be moving, and can't be at zero velocity.

You all got that? Haha.

And I guess I'll stop here for a while - I'll come back to explain further (in another post) why you need to be massless to move at the speed of light. :)

Derivator!

Look at this second-order equation:

How would you solve it? I mean, there’s always the conventional method of assuming a solution that has an exponential form, but did you know that you can treat this like a quadratic equation?

The method is known as the solution of second order differential equations via factorization, which isn’t really an original method thought out by me, but well, it helps to explain why the solution is of an exponential form. First of all, we factorize out the y term:

Then of course, we make a simplification; that is we allow:

And therefore we must insist that:

Of course, let us factorize this further:

In which case we must therefore have:

And of course if we solve for these two equations, we have:

And of course, the general solution being the sum of the two particular solutions we obtained earlier, from the principle of superposition for linear equations:

And if you only want a real solution, then:

And this explains why we always assume the solution is of an exponential form; simply because if you do solve it from first principles, it always is! :)

Resonance Imaging

So, some of you think Resonance Theory is outdated huh? Well, try this question! Do you think you can tell me which carbon atoms would most likely bear the positive charge in this cation without Resonance Theory:

I've drawn out the resonance hybrid (i.e. the actual molecular structure) of this ion. I'll give you a hint: there are four carbon atoms that could bear the positive charge. :)

------------------------------------------------

It seems like no one has given a go at this, but oh very well; if you can mentally draw the set of resonance structures in your head, this should really be problem at all:

And that's that! Haha.

Summation Woes

Well, here's something that both JX and Luoning can understand and appreciate; it's basically something I discussed with Shaun over MSN, and it's an alternating series, taking the form of:


Notice that we can group the terms like this and obtain a sum for an odd number of terms:


Also, we can group the terms like this and obtain a sum for an even number of terms:


The strange thing is, notice that if you consider an even number of terms, the sum goes to positive infinity, and if you consider an odd number of terms, the sum goes to negative infinity! This is what we call an oscillating series, which happens to be diverging as well.

I’ve included a graph for your reference, to illustrate the oscillating and diverging nature of this series:


Notice the diverging nature of the sum to n terms, and consequently, there can be no sum to infinity, simply because the sum to n terms depends on the very number of terms, and thus on the last term. A sum to infinity where the number of terms and the last term is not defined can therefore produce no well defined result.

Nuclear Worries

Nuclear worries should be of a small magnitude right? But it sure ain't. Sigh.

You know, one of the most interesting things about Nuclear Physics is that there’s no fixed boundaries that define the study of this field of Physics. What do I mean? Well, take Electrodynamics for instance: you have Maxwell’s Four Equations, that clearly set a basis from which all other theories of Electrodynamics are derived. For Classical Mechanics, there’s Newton’s Laws of Motions, and for Classical Dynamics, there’s the Lagrangian. So clearly, for these fields, there’s a fixed set of rules to go by.

But for Nuclear Physics, we base it on Quantum Mechanics (for the behavior of nuclei), Electrodynamics (for the charge distributions), Relativity (taking reduced mass and binding energies into account) and basic Mechanics and Dynamics (collisions etc.). So there’s really no limit to what can be done in this field.

Which explains why I’m actually finding myself doing so much for the Physics module I’m doing this semester, haha. So what does my Professor want me to figure out? Well, for now it’s Electrodynamics!

So my Professor goes and says this:

“The potential energy within a homogenously charged sphere of charge Q and radius R due to an interaction with another charge q within its interior at a distance r from its centre is given as:


And well, you all should know this already.”

I should? Well I sure don’t! So I’m going to try and derive it now instead of taking it for granted, haha.

Well so how do we start off? Easy, let us consider what we’re looking at in terms of a pictorial representation:


So what we have here is just a big blue sphere of charge Q, of radius R, and the small charge is placed within its interior, at a distance r away from the centre. So how do we go about solving this question? Well it’s easy – we assume the charge is homogenously distributed within the sphere, meaning each portion of the sphere bears the same amount of charge (i.e. uniform charge density ρ).

In that case, the charge q experiences the effective amount of charge that is contained within the bound radius of r instead of the whole sphere’s radius of R, marked out in pink:


In which case we can then write the electric force on the charge q as:


But we all know that the effective charge contained within the radius r is actually:


But we do know that the effective volume V of the pink region is:


And of course, the charge density is given by dividing the total charge Q by the total volume of the sphere:


Putting everything together:


The next part is to recognize that the Coulombic force is related to the potential energy as such:


And therefore conclude that:


So integrating this expression:


Now, to determine the constant k, we note first that when r = R, that is, where the small charge is on the surface of the big spherical charge, the potential energy is simply:


And therefore we must insist that:


Putting everything together:


Voila!

Arithmetic This!

There’s a special name for this type of sequence:


Notice that each term differs from its preceding and succeeding term by a constant difference of 3 – this type of series can be represented as such:


Where a is the first term, and d is the common difference. Notice that also that the n-th term is given by a + (n – 1)d. This is known as an Arithmetic Progression, or an Arithmetic Sum.

Now, can we find a sum to n terms? That means, can we find a general formula for the following summation of the first term to the last term:


Well, of course we can! Let us see how; first, let us consider the sum to n terms on its own:


We started off by writing the sum from the first term a – but we could have done so by starting from the last term A as well, and thus the sum to n terms written backwards from the last term
A is simply:


Now let’s put them side by side and add them up and let’s see if you notice something:


What do you notice? Well, notice that the ‘d’s and the ‘-d’s all cancel one another out, leaving us with:


The n is there because we have n terms in each sum, and adding up two sums should give us n of A and n of a. Now, what is the last term A in terms of the first term a? We’ve already said that we want the sum to n terms, and thus the last term A must be the n-th term, given by:


In which case we make a substitution:


And therefore the sum to n terms follows nicely:

Sweet eh? :)

Sum To Infinity, and Beyond!

Well, what exactly is a Geometric Progression? To put it very simply, it is a sum or series that has the following pattern:

Of course, you may then ask what is the sum to infinite terms, or the sum to infinity for this series, and we can then represent it as such:

The previous post dealt with the problem of 0.11111… as a recurring decimal using the idea of a Geometric Progression, and I’m about to show you exactly how right now.

First of all, let us consider the sum to n terms (this is often called the partial sum of the first n terms):

It must then be agreeable and logical that if I multiply this by the common ratio r, I obtain:

Taking the difference of the two, I see that:

And rearranging, I immediately see that:

Now what is the sum to infinity then? Easy, it can be evaluated by considering the limit as n tends towards infinity:

Notice that this limit can only exist, if the common ratio r has a magnitude smaller than one, such that it decreases to effectively zero for huge values of n:

With this in mind, the sum to infinity is simply:

So applying this to the previous problem, we see that:

And therefore there is no actual need for any algebraic manipulation to solve for recurring numbers once you have grasped this theory. :)