The interesting thing about this equation is that if we know the enthalpy of the system, we can then know the temperature dependence of the Gibbs free energy, which is very useful in many situations. For now, let us focus on the derivation of this relation. From first principles, we do a product rule differentiation, where we obtain:
 Now, using what we've all learnt in Physical Chemistry class, we have the following two relations:
Now, using what we've all learnt in Physical Chemistry class, we have the following two relations:If we do a simple substitution, we then obtain:
There you have it! A simple derivation of the relation, which holds for all systems, because we have made no mention of the system at all, and thus this must be a very general equation! (Am I the only one who's so excited about this result?) But you may ask: why would I need this result? And how would I use it? Good question!
Far too often one teaches the Gibbs-Helmholtz relation without any application, and I came up with a simple example to illustrate how to use this relation properly. Let us recall the definition of enthalpy:
And if we do a substitution into the Gibbs-Helmholtz relation, we obtain:
And therefore the result becomes:
We can now integrate this expression with respect to temperature, and we actually obtain a very neat expression:
If we graph this equation out, namely on a plot of G versus T, we obtain:
Interesting! Notice that there is a maximum point! To find this maximum point, we take the derivative of this graph (i.e. gradient function) and set it to zero:
We find that we end up with:

And solving for the temperature, we have:
But what does this entire analysis mean to us? Let us fall back to a more qualitative physical explanation: the Gibbs energy of an ideal gas is zero at absolute zero, because both its enthalpy and entropy are zero at this temperature. However, instead of the Gibbs energy decreasing when temperature is raised, the Gibbs energy increases initially! This is counter-intuitive if one thinks of the Gibbs energy as the amount of work available - shouldn't this decrease when the temperature is raised because at higher temperatures there is more entropy?
This just means that at lower temperatures, the enthalpy content must be larger than the entropy content! Which makes sense! Because of a lower entropy, more work can actually be harnessed from a system. But what's the drawback? Your system can't really do much work in the first place!
In such a case the two laws of Thermodynamics tells men that they are not real masters, for the 1st law says that you can only break even, but the 2nd law says that you can't even win!
This situation also allows us to determine the absolute entropy of an ideal gas! Recall that the slope of the graph was calculated previously, but this slope of the graph is the derivative of the Gibbs function with respect to temperature, which in effect, is the negative of the entropy! Therefore we see that:
 Since the term in parentheses must be negative when T is lesser than 1, and entropy is never negative, we must insist that c must be a negative term!
Since the term in parentheses must be negative when T is lesser than 1, and entropy is never negative, we must insist that c must be a negative term!Perhaps one might wish to work out a more exact relation for a Dieterici gas? Or perhaps a van der Waals gas?
Heh. Try it!








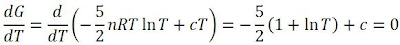


No comments:
Post a Comment