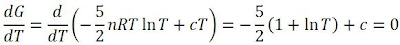Enthalpical Feat

Here's a very good question:

We all know that the enthalpy of vapourization varies with temperature, that is for a phase transition of the form A(l) to A(g), the enthalpy change ΔH will generally change with temperature. Therefore, the question in mind is: what do you think the value ΔH for vapourization is when the temperature tends towards infinity?

A good Physical chemist should have a good gut feeling! :p

Entropical Catharsis

If you haven't noticed, I'm sticking to a very wise mantra by posting short tidbits these few days:

"A man of few words... is a wise man!"

Very true indeed - I often find myself the butt of all jokes whenever I open my mouth too many times.

In any case, I was reading an excerpt from a Statistical Mechanics book when it occurred to me just how much I've changed in the past four or five years:

*Back then in Physics Olympiad training tutorials with Mr Daniel Khor*

YYK: ".... alright, remember this Yong Kiat, entropy change is good if it's positive! Because that's the correct answer, can get you marks!"

*Now after 4,5 years...*

YYK: "Oh man, entropy goes up again. We're screwed. This sucks. We're all going to die."

Haha, heat death of the Universe never did sound appealling to me, just that I was always too caught up in getting the right answer.

Absolute Zero Ain't Zero-Point

I was just wondering:

"Even when the temperature reaches 0 K, atoms in a solid still manage to vibrate with a zero-point energy..."

It's as if even when all of the energy has been sapped from particles, the particles are still resilient, showing us that there is some forbidden life-energy that cannot be touched no matter how low the temperature goes. It's amazing isn't it? It's as if everything around us has some fundamental life-force!

Reminds me of a verse from the bible, but too bad I can't remember it. :p

Water (II): Resilience

I just checked out Mount Everest's height at Wikipedia, and it's at a staggering height of 8,840 m! You know what that means?

That means I, weighing 95 kg, would need approximately 8840(95)(9.81) = = 8238438 J of energy to scale that mountain fully! What a heck of a mountain!

Now just look at this: let's say I have 62.5 moles of water - that isn't very much, just about 1 litre of pure water. Assuming it is at room temperature, and assuming that I need very hot water at 373.15 K to make good hot chocolate for my family, the energy I need is given by a simple calculation:



I've done the above calculation assuming that the boiling process was done at constant volume inside a simple flask, and I used the latent heat of vapourization and specific heat capacity of water, as above. I mean, you probably won't boil away all the water right?

What in the world? I climb so high up, and all the energy I expended, can only be used to boil 3 litres of water? This is ridiculous!

Indeed. Heh. :p

Granted of course, I've neglected the inefficiency of the human body, the heat loss from the body due to the cold, the sapping of mental strength, the time loss due to sleep, as well as the energy loss because of additional weight (i.e. equipment). So the above calculation isn't really anything actually. :p

Pre-Eminent Molecule: Water (I)

God uses water in the bible, in very powerful ways - He used water to flood the Earth in the Noah's Ark saga; water is used for baptism, even to baptise Jesus; Jesus turned water to wine; Jesus and Peter both walked on water itself; Moses knocked his staff on a rock and water came out, springing forth life, that quenched the dying Israelites' thirst and the list is endless! The bible makes so many referenes to the humble water molecule, and it's a really incredible molecule!

I bet you the only reason why it's such an unsung hero in our lives is because it seems to have an ubiquitous existence, and that's why we tend to take the precious water we have for granted. I feel that Singaporeans have themselves taken the potable water flowing out of their taps for granted, myself inclusive.

Therefore, inspired by my friend, Shaun Lin Darong, I shall now start posting a series of posts on the water molecule, and the first post is a simple one, to whet all of your appetites: have you ever wondered why the water molecule can only accept a single proton when it has two lone pairs of electrons?

What I'm trying to say is, why can't the following reaction occur:



After all, water has two lone pairs of electrons right? So why not? A seasoned Chemistry student would simply retort: Of course it can't! The first protonation results in a positive charge on the water molecule, which naturally repels the addition of another positively charged proton!

However, another could simply argue - then if I just increase the concentration of acid in water, eventually this will result in both lone pairs of electrons on the oxygen being protonated right?

And the argument could go on endlessly in fact, and we'd have no idea who's right! The problem with such arguments is that all of them are purely qualitative explanations, and there is no rigour to back them up at all. So how should we go about solving this problem?

Easy, we fall back to first principles: we do a simple molecular orbital calculation! All will come to light when we analyse the water molecule from its very fundamental electronic structure, and here goes:

Water is a simple triatomic bent molecule, with a bond angle of 109.5 degrees - upon closer examination, we see that its point group is C2v, such that we say it has C2v symmetry:

I've included the symmetry operations above for reference, and here is the associated character table for C2v molecules:

So let's start assigning each irreducible representation in the table to each orbital in the three atoms of water! Let's however, not forget one postulate in molecular orbital theory, that in order to form bonds, orbitals must go into overlap effectively, both in a spatial and energetical sense. However, this means that the only orbitals in effective overlap will be the valence orbitals, since the inner core orbitals are buried deep within the atoms. Therefore in our analysis, we shall only consider the valence orbitals of both oxygen and hydrogen atoms.

If so, let us then consider the symmetry labels of the oxygen valence atomic orbitals first, where we concern ourselves with the 2s and three 2p orbitals. Taking a look at the 2s atomic orbital of the central oxygen atom, we see that:

Indeed, it has a symmetry label of a1, corresponding to the totally symmetric irreducible representation of A1, since all operations result in the same 2s orbital. If we take a look at the 2pz orbital, we find that it also has the a1 symmetry label:

The 2px and 2py orbitals however, have symmetry labels of b1 and b2 respectively, because they correspond to the irreducible representations of B1 and B2 respectively (please verify this yourself by looking at the diagrams below and performing the symmetry operations yourself!):

If so, then we can summarise everything in a single table, on the oxygen atomic orbitals:

It is now time to take a look at the hydrogen atomic orbitals, namely the 1s atomic orbitals; however, we require not the 1s atomic orbitals but rather, a symmetry-adapted linear combination of the 2 1s atomic orbitals, which means that we could either have an additive linear combination, or a subtractive linear combination (note that this is only the case for simple additions of two atomic orbitals, since these are the only two combinations that can result). The SALCs are illustrated below:

I coloured them differently to show whether they're in phase or not, and leaving the verification to the reader, these two SALCs have symmetry labels of a1 (additive linear combination) and b2 (subtractive linear combination), and thus we summarise this in a table again:

So let's plot the molecular orbital energy level diagram:

One now easily sees that the b1 molecular orbital is non-bonding, indicating a lone pair of electrons centred on the oxygen atom a la 2px fashion. Where is the other lone pair of electrons? Easy, it's the lowest a1 molecular orbital, which is also non-bonding (notice it isn't lowered very much in energy), which has the the form of a 2s atomic orbital centred on the oxygen as well.

But what does this mean? Notice that the b1 molecular orbital has an energy of -13.6 eV, which is just nice for the bonding to a proton, whose energy is also at -13.6 eV! Howevr, the lowest a1 molecular orbital is simply too low in energy (i.e. too unreactive) to even bond with a proton, and therefore we expect only one proton to be able to bind, for there is only one reactive binding site.

Wow. This post has been heavy on graphics. :p

Final Fantasy Elixir: Ethers

I was thinking, what better way to revise for Organic Chemistry, than to share it with others on this blog? Plus, all my peers in Chemistry will be reading this blog, so I guess it's the best way to learn Chemistry!


Alright, here goes!


Let's start off with the synthesis of ethers; we've learnt that alcohols undergo an intramolecular dehydration in order for it to become alkenes, but did you know that alcohols can also undergo an intermolecular dehydration to become ethers? From my point of view, this is the easiest way to partition your way of thinking in order to better understand the two competing reactions.


Of course, there are other ways, heh. But let us just keep this point in view for the moment: only primary alcohols may actually undergo such a dehydration reaction to produce ethers.


The fundamental difference between alkene-dehydration and ether-dehydration is that while the former is a simple elimination reaction, the latter is a simple nucleophillic substitution reaction, in particular a SN2 reaction. The nucleophile in this reaction is the alcohol itself, and the substrate is a protonated alcohol, an alkyloxonium ion.


Recall also that elimination reactions are favoured at higher temperatures, and this explains why the alkene forms when the reaction is carried out at 180 degrees, and the ether forms when the reaction is carried out at 140 degrees.


As shown above, the first step is a simple acid-base reaction, where the lone pair of the alcoholic oxygen functions as a base that forms a bond to a proton from the concentrated sulphuric acid. This grants the oxygen a positive charge that polarises and weakens all bonds connected to oxygen. The alcohol, being in excess as the solvent and reactant, functions as a nucleophile (now that the hydroxy group has been converted to a better leaving group) and attacks the hydroxy carbon in a SN2 mechanism (a.k.a back-side attack!) in a single step to produce the protonated ether (you can call it a dialkyloxonium ion as well!). The last deprotonation step is then carried out by other alcohol molecules.


However, this method of synthesis is only good for industrial synthesis of large amounts of ether, and has some very obvious limitations. For instance, unsymmetrical ethers are almost impossible to synthesise with a very precise degree of control! Look at the following example:


Indeed, if two different alcohols are used, then three possible ethers can be formed! Such lack of control is definitely not a desirable quality of synthesis reactions. Moreover, let us consider another important factor - by virtue of the fact that this is a simple SN2 reaction, it means that secondary and tertiary alcohols are unlikely substrates, because using them leads to the hindering of the formation of the transition state, and therefore, elimination is favoured instead, resulting in alkenes as the major product.


A much better synthesis route is known as the Williamson-Synthesis, a rather simple trick but oh-so-effective! Just take a look:

The leaving group L can simply be any good leaving group, such as a tosylate or even a halide group. Notice that it is simply another SN2 reaction, but one uses a much stronger nucleophile, and one uses a much better leaving group in the substrate! It's just playing around with mechanisms, really! This is a much better method for producing asymmetric ethers, because there is no ambiguity to the structure of the ether that may be formed!


However, if this is still a SN2 reaction, then the usual limitations hold for this reaction scheme as well. What I mean to say is, if the substrate is a secondary or tertiary halide, then elimination is bound to occur significantly. Therefore, one must use proper conditions such as the choice of an aprotic polar solvent, lower temperatures etc. to favour the SN2 reaction. In which case, if you want to form an asymmetric ether that has a bulky alkyl group R1 on one side and a relatively unhindered alkyl group R2 on the other side, one should use a R2 alkyl halide and a R1 base for the synthesis to favour a SN2 reaction.


There is also another class of ethers that are very special, which we term as epoxides, which is simply a short-form nomenclature for epi-oxide molecules, a three-membered ether ring, which is also known as an oxirane, as follows:


A very easy method to synthesise such epoxides is to use an alkene and a peroxycarboxylic acid, where the acid actually forms a cyclic transition state with the pi-bond of the alkene, and the mechanism is a single concerted step where all bonds break and reform at once:


We can therefore think of the acid as being a very good electrophile, and the alkene being the nucleophile in this reaction!


Now, because there is a three-membered ring, such epoxides are rendered highly susceptible to nucleophillic substitution due to the ring strain (i.e. it is favourable to break the ring that is highly strained), and this can be done in two ways, via an acid-catalysis or a base-catalysis.


The acid catalysis mechanism involves the protonation of the epoxide oxygen on the lone pair of electrons, resulting in a better leaving group, and also polarises the bonds connected to oxygen. The nucleophile in this case, is water - notice that this type of catalysis makes the hydrolysis easier because a better leaving group and a more reactive carbon centre is formed.


Notice that the reactive substrate is a protonated epoxide, meaning that the intermediate has a positive charge. Similarly, this means that the transition state involves a species with a positive charge that needs to be dispersed effectively. Indeed! One notices that if an asymmetric epoxide is being used in this reaction, the two oxygen-carbon bonds are of different length - in fact, the oxygen forms a weaker bond to the carbon that is more able to retain a positive charge (i.e. the more highly alkyl substituted carbon atom).


In fact, in the transition state, it is this bond that breaks, because then the carbon is more able to disperse its developing positive charge as the nucleophile attacks. Therefore acid catalysis usually results in the more hindered carbon being attacked (but not exclusively though!).


The base catalysis mechanism doesn't invoke the use of a better leaving group - it focusses much more on providing a high concentration of a very strong nucleophile that does the attack (in this case, a hydroxide ion). Notice that the leaving group is highly basic (an alkyloxonium ion) that immediately protonates itself in water to stabilise itself.


However, this attack is more of a nucleophillic nature, and therefore we see that it is a simple SN2 intramolecular reaction (sort of!). As such, the nucleophillic prefers to attack the more unhindered carbon atom.

And well, I guess I've run out of things to say. :p

WTH - What The Helmholtz!

Yes, one of the many great names embedded into Thermodynamics, and one often wonders what one has to do to engrave his name into the annals of history. Well, let us take a look at what Gibbs and Helmoholtz formulated, which van't Hoff eventually utilized to derive his very own van't Hoff equation. We're going into a very useful relation in Thermodynamics, which is known as the Gibbs-Helmholtz Relation, which is simply:

The interesting thing about this equation is that if we know the enthalpy of the system, we can then know the temperature dependence of the Gibbs free energy, which is very useful in many situations. For now, let us focus on the derivation of this relation. From first principles, we do a product rule differentiation, where we obtain:

Now, using what we've all learnt in Physical Chemistry class, we have the following two relations:

If we do a simple substitution, we then obtain:

There you have it! A simple derivation of the relation, which holds for all systems, because we have made no mention of the system at all, and thus this must be a very general equation! (Am I the only one who's so excited about this result?) But you may ask: why would I need this result? And how would I use it? Good question!

Far too often one teaches the Gibbs-Helmholtz relation without any application, and I came up with a simple example to illustrate how to use this relation properly. Let us recall the definition of enthalpy:

For a monoatomic ideal gas, we must also agree that:

And if we do a substitution into the Gibbs-Helmholtz relation, we obtain:

And therefore the result becomes:

We can now integrate this expression with respect to temperature, and we actually obtain a very neat expression:

If we graph this equation out, namely on a plot of G versus T, we obtain:

Interesting! Notice that there is a maximum point! To find this maximum point, we take the derivative of this graph (i.e. gradient function) and set it to zero:

We find that we end up with:

And solving for the temperature, we have:

But what does this entire analysis mean to us? Let us fall back to a more qualitative physical explanation: the Gibbs energy of an ideal gas is zero at absolute zero, because both its enthalpy and entropy are zero at this temperature. However, instead of the Gibbs energy decreasing when temperature is raised, the Gibbs energy increases initially! This is counter-intuitive if one thinks of the Gibbs energy as the amount of work available - shouldn't this decrease when the temperature is raised because at higher temperatures there is more entropy?

This just means that at lower temperatures, the enthalpy content must be larger than the entropy content! Which makes sense! Because of a lower entropy, more work can actually be harnessed from a system. But what's the drawback? Your system can't really do much work in the first place!

In such a case the two laws of Thermodynamics tells men that they are not real masters, for the 1st law says that you can only break even, but the 2nd law says that you can't even win!

This situation also allows us to determine the absolute entropy of an ideal gas! Recall that the slope of the graph was calculated previously, but this slope of the graph is the derivative of the Gibbs function with respect to temperature, which in effect, is the negative of the entropy! Therefore we see that:

Since the term in parentheses must be negative when T is lesser than 1, and entropy is never negative, we must insist that c must be a negative term!

Perhaps one might wish to work out a more exact relation for a Dieterici gas? Or perhaps a van der Waals gas?

Heh. Try it!