Sum To Infinity, and Beyond!

Well, what exactly is a Geometric Progression? To put it very simply, it is a sum or series that has the following pattern:

Of course, you may then ask what is the sum to infinite terms, or the sum to infinity for this series, and we can then represent it as such:

The previous post dealt with the problem of 0.11111… as a recurring decimal using the idea of a Geometric Progression, and I’m about to show you exactly how right now.

First of all, let us consider the sum to n terms (this is often called the partial sum of the first n terms):

It must then be agreeable and logical that if I multiply this by the common ratio r, I obtain:

Taking the difference of the two, I see that:

And rearranging, I immediately see that:

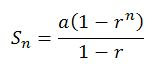
Now what is the sum to infinity then? Easy, it can be evaluated by considering the limit as n tends towards infinity:

Notice that this limit can only exist, if the common ratio r has a magnitude smaller than one, such that it decreases to effectively zero for huge values of n:

With this in mind, the sum to infinity is simply:

So applying this to the previous problem, we see that:

And therefore there is no actual need for any algebraic manipulation to solve for recurring numbers once you have grasped this theory. :)