However, let us first consider the importance of entropy - what exactly is this monster called entropy? Well, as all elementary definitions put it, entropy is the amount of disorder within a system. So if you have a cup of hot water, and cup of cold water, naturally the hot water will have its molecules sloshing around (alright, not quite literally) with kinetic motion, far more than the cold miserable molecules of the cold water would. As such, by virtue of its internal molecular motion, we say that the hot water has more entropy of motion because of a higher temperature.
Yeah yeah, so it's disorderliness, so what? Sure enough, that's not all. Let us then dive into the Second Law of Thermodynamics again, in its simplest form: the entropy of the universe must always increase in an irreversible process. Ah, but why must entropy increase? This is always a difficult concept to explain, and thus let us have a thought experiment:
If I have a container with a partition separating hot and cold water, I say that the hot water is a region of higher entropy, and the cold water a region of lower entropy - but is this really the state of maximum entropy? No! Why? Because there exists a very obvious sense of order! Because the container can be exactly divided into an ordered region and a disordered region, and therefore, there is an intrinsic order associated with the system!
So how would I increase the entropy further? Easy, break that orderliness! So we break the partition and allow the regions to mix, producing lukewarm water, and thereby increase the entropy of the system to a maximum. Now, ask yourself - this is an irreversible process, is it not? You will never see a lukewarm glass of water separating itself into hot and cold regions spontaneously by itself! No way man! And the direction of increasing entropy tells us how this works.
Now, let us consider this again: why is entropy so important? Think about it: the hot water and cold water have internal energy U - this internal energy can be used to do work, because the hot water has thermal energy that can be used to generate electricity by perhaps, driving a thermocouple.
Now consider the hot and cold water mixing - it still has internal energy U right? But yet the amount of work it can do is lesser! When you use warm water to drive a thermocouple, not so much energy is produced as work because the temperature isn't that high.
Weird! The amount of internal energy available is the same, but yet the amount of work that can be done is different! And this is explained because of entropy. As entropy increases, what this means is that the energy contained within a system is more spread out.
Ask yourself again: what kind of energy is useful? Why, of course, it must be energy that is able to flow from one region to another, energy that can flow! If energy can't be transported or unable to flow, then we simply can't tap it or harness it! Imagine if the chemical energy from your food couldn't be moved from the food itself into your cells for you to utilize! You'd be unable to do anything with the food you ate!
Entropy causes a spreading of the energy into an equilibrium state, such that there is an even mix of energy (and mass) everywhere within the system, such that in such an even distribution of energy, energy can't move anymore! Or rather, if energy moves in one direction, an equal amount will move in the opposite direction that compensates such movement, and thus there is no net movement of energy observable. Work is the net movement of energy, a loose definition, and if energy can't even move, work can never be done. Of course work has a more rigorous definition, but oh well, it's sufficient for this point.
Well, here comes the main point of this post, to prove (in a very non-rigorous manner) that entropy is also a function of time. Please bear with me as I plough you through some essential basics before that. Let us first take a look at how the change in entropy (dS) is mathematically defined in basic Thermodynamics:
Simple enough, a change in entropy (dS) is caused by a reversible flow of heat (dQrev) in or out of the system, divided by the temperature of the system (T). If the flow of heat is into the system, then dQrev is postive, otherwise it's negative. The reason why it's defined like this can't be explained using any simple ideas, but suffice it to say (the mathematical derivation is very complex and time consuming) that heat is the flow of energy brought about by molecular motion, which therefore increases the disorderliness of the system. As such, we use the flow of heat as a measure of the change in entropy of the system.
The temperature is present in the equation because obviously for a very high temperature a small flow of heat wouldn't cause that much significant a change in the entropy of the system. Thus in Physics one would say that entropy change is a change weighted by the temperature of the system.
Let us now first prove an important theorem in Thermodynamics, the Clausius Inequality, which actually shows that no matter what, as long as you have a cycle, the entropy of the universe must definitely increase! Interesting right, a proof! Now let's first start from the First Law of Thermodynamics, which states that:
This means the change in internal energy of a system is equal to the heat flow in/out of the system and the work done on/by the system. Notice that this two quantities can be either reversible (rev) or not. We then make the distinction between reversible work done on the system and irreversible work done on the system:
That is, reversible work done on the system is lesser or equal to the irreversible work done on the system. The equality holds only when the work done is reversible, in which case a subscript rev is added to dW. And if we do some mathematical arrangement, we see that:
Which must lead us to the conclusion that:
And therefore we have:
Which tells us that if we divide throughout by the absolute temperature of the system we obtain:
And recognising that the quantity on the left is simply the change in entropy, we write:
And we proceed to determine the total change in entropy when we have a cycle, by integrating over the cycle, which is indicated with a small circle on the integral to indicate a closed integral:
And recall by definition that a cycle is a process that brings a system from state A to some state, and then back to state A. If entropy is a state function, then the system being at state A, will possess a fixed entropy, and thus the change in entropy of the system must be zero since the final and initial entropy of the system is the same:
Which concludes the derivation of the Clausius Inequality:
So what exactly does this inequality mean? Well, you must notice that if the entropy change of the system is zero, then we must agree that change in entropy of universe = change in entropy of surroundings, am I right? Now look at the equation above: it says that the heat flow is always negative in a cycle, and therefore the heat that flows must flow out of the system into the surroundings.
Wait a minute, doesn't the heat flowing into the surroundings mean that the surroundings' entropy change must be positive? Hey that means that the entropy change of the universe increases right?
Correct! In any cycle, we end up increasing the entropy of the universe - we can't go against this principle. This means that everytime you turn on and use the engine in your car, you're killing the universe. :p
---------------------------------------------------------
As for time-based entropy, let us consider the change in entropy again:
Then using the chain rule in basic calculus, we have:
Which then rearranges into:
We have recognised that dQrev/dt simply refers to power, and we explicitly refer to power as a function of time by putting the bracket Prev(t). And from the previously worked out example, we have:
Which allows us to say:
So that we can conclude that:
In other words, the entropy changes with time because heat must flow as a function of time! If there exists no time for heat to flow, there can be no change in entropy. This last equation took for granted that the power is always causing heat flow into the system, which is not necessarily true, but it's just a special case anyway. :p
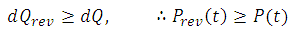
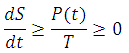
Therefore, by knowing the mathematical form of P(t), we can simply integrate within the limits, and obtain entropy as a function of time. Which is actually easily done if we consider heat transmission via radiation. The law of heat transmission by radiation is summed up in the Stefan-Boltzmann Law of Radiation, where:
And there you have it, you actually can express the entropy of a system as a function of time (notice in the above I omitted the constant of integration because I'm lazy, :p).
No comments:
Post a Comment